Booth's Algorithm을 이용한 음수 곱셈

과제로 부스 알고리즘을 사용해 볼 일이 있어서 알아봤는데 굉장히 흥미로웠다. 처음엔 오른쪽 시프트하고 부호 어떻게 채우는지 이해가 안돼서 굉장히 고생함ㅠㅠ

1. Booth's 알고리즘이란?

부호가 있는 이진수의 곱셈을 수행할 수 있도록 해주는 알고리즘으로, 영국의 컴퓨터과학자인 Andrew Donald Booth에 의해 개발되었다. 계산을 하기 전 계산에 사용되는 수에 대해 알아보자.

1.1. Booth's Algorithm을 이용한 계산에 사용되는 수

M x Q를 계산한다고 가정하자. 

• M = Multiplicant
• Q = Multiplier
• A = M의 bit수만큼 0으로 초기화한 후 계산에 사용하는 친구
• q0 = 계산에 사용하는 최하위 비트
• Count = loop를 돌리는 횟수로 계산하려는 2진수의 bit수이다.

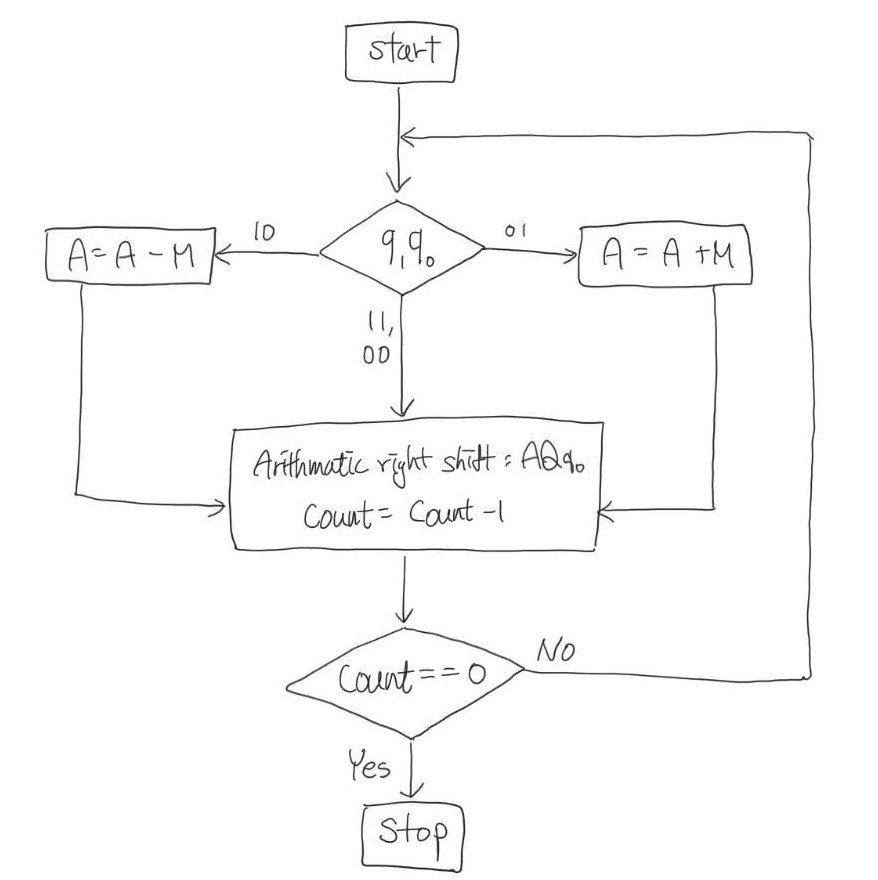
1.2. Flowchart

아래 사진의 순서에 따라 loop를 돌며 곱셈의 결과를 도출할 것이다. 아래 예제를 보자.

2. Booth's 알고리즘을 이용한 음수 곱셈

2.1. 계산에 필요한 수 초기화 및 대입

(-12) x (30)을 6bits 곱셈으로 계산해 볼 것이다. 위 규칙에 따라 아래와 같이 초기화된다.

• M = -12의 2진수 표현 = 110100
• Q = 30의 2진수 표현 = 011110
• A = M의 bit수인 6자리를 0으로 초기화 = 000000
• q0 = 0으로 초기화 = 0
• Count = 계산하려는 2진수의 bit수 = 6

2.2. 계산과정

우리는 2.1.에서 정의한 'AQq0'를 Count만큼의 loop를 돌며 계산해 나갈 것이다. 

총 곱셈 과정에서 수행할 연산은 2's complement, Arithmatic right shift, 이진수 덧셈 세가지밖에 없으니 겁먹지 않아도 된다.

 

 

<모든 초기화가 끝난 상태>

Count	A	Q(q6 q5 q4...q1)	q0	설명
6	000 000	011 110	0	모든 수를 초기화했다.

이제 우리는 flowchart에서 봤던 것처럼 q1q0값이 무엇인지에 따라 아래 표를 채워나갈 것이다. 

현재 q1q0은 00이므로 flowchart의 아래로 내려가 AQq0에 대해 Arithmatic right shift를 수행하고 Count를 감소시킬 것이다.

 

 

<Count == 5 를 계산하는 중>

Count	A	Q(q6 q5 q4...q1)	q0	설명
6	000 000	011 110	0	모든 수를 초기화했다.
5	000 000	001 111	0	q1q0가 00이므로 보라색 비트 시프트 후 Count 내림

다음 q1q0는 이제 10으로 바뀌었다. 이번에는 flowchart의 왼쪽 화살표를 따라가 A = A - M 연산을 수행해야 한다.

A는 000 000이고 -M은 12, 즉 이진수로 001 100이다. 둘을 더하면 001 100일 것이다.

A = A - M 연산과 A = A + M 연산은 둘 다 덧셈 연산이다.
-M을 더하는지 M을 더하는지만 다르다고 생각하면 된다.

 

덧셈 계산을 수행한 다음 Arithmatic right shift를 수행하고 Count를 감소시켜야 한다. 

그 후 과정은 위에서 예시를 보였던 연산이므로 넘어가겠다.

Arithmatic right shift 연산을 할 때 왼쪽 공간에 채우는 숫자는 
A가 양수일 경우, 즉 첫비트가 0일 경우 0으로 채운다.
A가 음수일 경우, 즉 첫비트가 1일 경우 1으로 채운다.

 

 

<Count == 1 를 계산하는 중>

Count	A	Q(q6 q5 q4...q1)	q0	설명
6	000 000	011 110	0	모든 수를 초기화했다.
5	000 000	001 111	0	q1q0가 00이므로 보라색 비트 시프트 후 Count 내림
5	001 100	001 111	0	q1q0가 10이므로 A = A - M 연산 수행
4	000 110	000 111	1	파란색 비트 시프트 후 Count 내림
3	000 011	000 011	1	q1q0가 11이므로 연두색 비트 시프트 후 Count 내림
2	000 001	100 001	1	q1q0가 11이므로 노란색 비트 시프트 후 Count 내림
1	000 000	110 000	1	q1q0가 11이므로 주황색 비트 시프트 후 Count 내림

이번에는 q1q0가 01이 나왔으므로 A = A + M을 수행해야 한다.

M은 (-12)로, 이진수로는 110 100이다. 현재 A인 000 000과 더해주면 110 100이 나온다.

따라서 다음 A는 110 100이다. 계산을 마무리해 보자.

 

 

<완성된 표>

Count	A	Q(q6 q5 q4...q1)	q0	설명
6	000 000	011 110	0	모든 수를 초기화했다.
5	000 000	001 111	0	q1q0가 00이므로 보라색 비트 시프트 후 Count 내림
5	001 100	001 111	0	q1q0가 10이므로 A = A - M 연산 수행
4	000 110	000 111	1	파란색 비트 시프트 후 Count 내림
3	000 011	000 011	1	q1q0가 11이므로 연두색 비트 시프트 후 Count 내림
2	000 001	100 001	1	q1q0가 11이므로 노란색 비트 시프트 후 Count 내림
1	000 000	110 000	1	q1q0가 11이므로 주황색 비트 시프트 후 Count 내림
1	110 100	110 000	1	q1q0가 01이므로 A = A + M 연산 수행
0	111 010	011 000	0	빨간색 비트 시프트 후 Count 내림

loop의 종료 조건인 Count == 0 이 만족되어 연산이 모두 끝났다.

AQ가 연산의 결과로, 111 010 011 000이 나왔다.

이 수의 2의 보수는 십진수로 확인해보면 000 101 101 000 = 256 + 64 + 32 + 8 = 360으로, 

(-12) x (30) = -360이 제대로 계산되었음을 알 수 있다.